Pc-Saturation & Relative Permeability Functions¶
How To Test Characteristic Curves¶
The CHARACTERISTIC_CURVES card allows testing of the specific capillary
pressure-saturation functions and relative permeability functions chosen for
the simulation. Testing can be done by including the keyword TEST
within the CHARACTERISTIC_CURVES block. Including this keyword will produce
output (.dat files) which provides (a) the capillary pressure for the entire
range of liquid saturation, (b) the liquid saturation for the entire range of
capillary pressures, (c) the analytical derivative of liquid saturation with
respect to the capillary pressure, (d) the numerical derivative of liquid
saturation with respect to the capillary pressure, (e) the liquid relative
permeability values for the range of liquid saturation, (f) the gas relative
permeability values for the range of liquid saturation, and the (g) analytical
and (h) numerical derivatives of the relative permeability functions with
respect to liquid saturation.
Example¶
CHARACTERISTIC_CURVES cc1 SATURATION_FUNCTION VAN_GENUCHTEN LIQUID_RESIDUAL_SATURATION 0.d0 M 0.5d0 ALPHA 1.d-4 MAX_CAPILLARY_PRESSURE 1.d6 / PERMEABILITY_FUNCTION MUALEM_VG_LIQ LIQUID_RESIDUAL_SATURATION 0.d0 M 0.5d0 / PERMEABILITY_FUNCTION MUALEM_VG_GAS LIQUID_RESIDUAL_SATURATION 0.d0 GAS_RESIDUAL_SATURATION 1.d-40 M 0.5d0 / TEST /
Including the TEST keyword in the CHARACTERISTIC_CURVES block, as shown
above, will produce the following output files, shown as examples only:
pflotran_sat_pc.dat:
"saturation", "capillary pressure" 0.000000E+00 1.000000E+09 1.000000E-02 1.000000E+09 2.000000E-02 1.000000E+09 3.000000E-02 1.000000E+09 4.000000E-02 1.000000E+09 5.000000E-02 1.000000E+09 6.000000E-02 1.000000E+09 7.000000E-02 1.000000E+09 8.000000E-02 1.000000E+09 9.000000E-02 1.000000E+09 1.000000E-01 1.000000E+09 1.100000E-01 1.000000E+09 1.200000E-01 1.000000E+09 1.300000E-01 1.000000E+09 1.400000E-01 1.000000E+09 1.500000E-01 1.000000E+09 1.600000E-01 7.593750E+08 1.700000E-01 3.513358E+08 1.800000E-01 1.802032E+08 1.900000E-01 1.000000E+08 2.000000E-01 5.904900E+07 ... ...
pflotran_pc_sat.dat:
"capillary pressure", "saturation", "dsat/dpres", "dsat/dpres_numerical" 1.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 2.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 3.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 4.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 5.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 6.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 7.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 8.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 9.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 1.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 2.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 3.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 4.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 5.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 6.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 7.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 8.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 9.000000E+01 1.000000E+00 0.000000E+00 0.000000E+00 1.000000E+02 1.000000E+00 0.000000E+00 0.000000E+00 2.000000E+02 1.000000E+00 0.000000E+00 0.000000E+00 ... ...
pflotran_liquid_rel_perm.dat:
"saturation", "liquid relative permeability", "liquid dkr/dsat", "liquid dkr/dsat_numerical" 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 1.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 2.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 3.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 4.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 5.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 6.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 7.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 8.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 9.000000E-02 0.000000E+00 0.000000E+00 0.000000E+00 1.000000E-01 0.000000E+00 0.000000E+00 6.969172E-46 1.100000E-01 2.203846E-15 1.652884E-12 1.652943E-12 1.200000E-01 3.989387E-13 1.496020E-10 1.496049E-10 1.300000E-01 8.348157E-12 2.087039E-09 2.087069E-09 1.400000E-01 7.221562E-11 1.354043E-08 1.354058E-08 1.500000E-01 3.849960E-10 5.774940E-08 5.774996E-08 1.600000E-01 1.511178E-09 1.888972E-07 1.888989E-07 1.700000E-01 4.801937E-09 5.144933E-07 5.144973E-07 1.800000E-01 1.307242E-08 1.225540E-06 1.225549E-06 1.900000E-01 3.162278E-08 2.635231E-06 2.635249E-06 2.000000E-01 6.969172E-08 5.226879E-06 5.226913E-06 ... ...
pflotran_gas_rel_perm.dat:
"saturation", "gas relative permeability", "gas dkr/dsat", "gas dkr/dsat_numerical" 0.000000E+00 1.000000E+00 0.000000E+00 0.000000E+00 1.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 2.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 3.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 4.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 5.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 6.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 7.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 8.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 9.000000E-02 1.000000E+00 0.000000E+00 0.000000E+00 1.000000E-01 1.000000E+00 0.000000E+00 -6.250000E-01 1.100000E-01 9.937136E-01 -6.333929E-01 -6.333930E-01 1.200000E-01 9.873154E-01 -6.469643E-01 -6.469643E-01 1.300000E-01 9.807617E-01 -6.643325E-01 -6.643327E-01 1.400000E-01 9.740181E-01 -6.848812E-01 -6.848814E-01 1.500000E-01 9.670549E-01 -7.082013E-01 -7.082015E-01 1.600000E-01 9.598459E-01 -7.339817E-01 -7.339819E-01 1.700000E-01 9.523679E-01 -7.619671E-01 -7.619673E-01 1.800000E-01 9.445999E-01 -7.919370E-01 -7.919373E-01 1.900000E-01 9.365232E-01 -8.236948E-01 -8.236951E-01 2.000000E-01 9.281207E-01 -8.570601E-01 -8.570604E-01 ... ...
By plotting these output files against the equations documented under Capillary Pressure - Saturation Functions and Relative Permeability Functions, a visual comparison can be made of the accuracy of the implemented characteristic curves within PFLOTRAN.
Testing Results For Pc-Saturation Functions¶
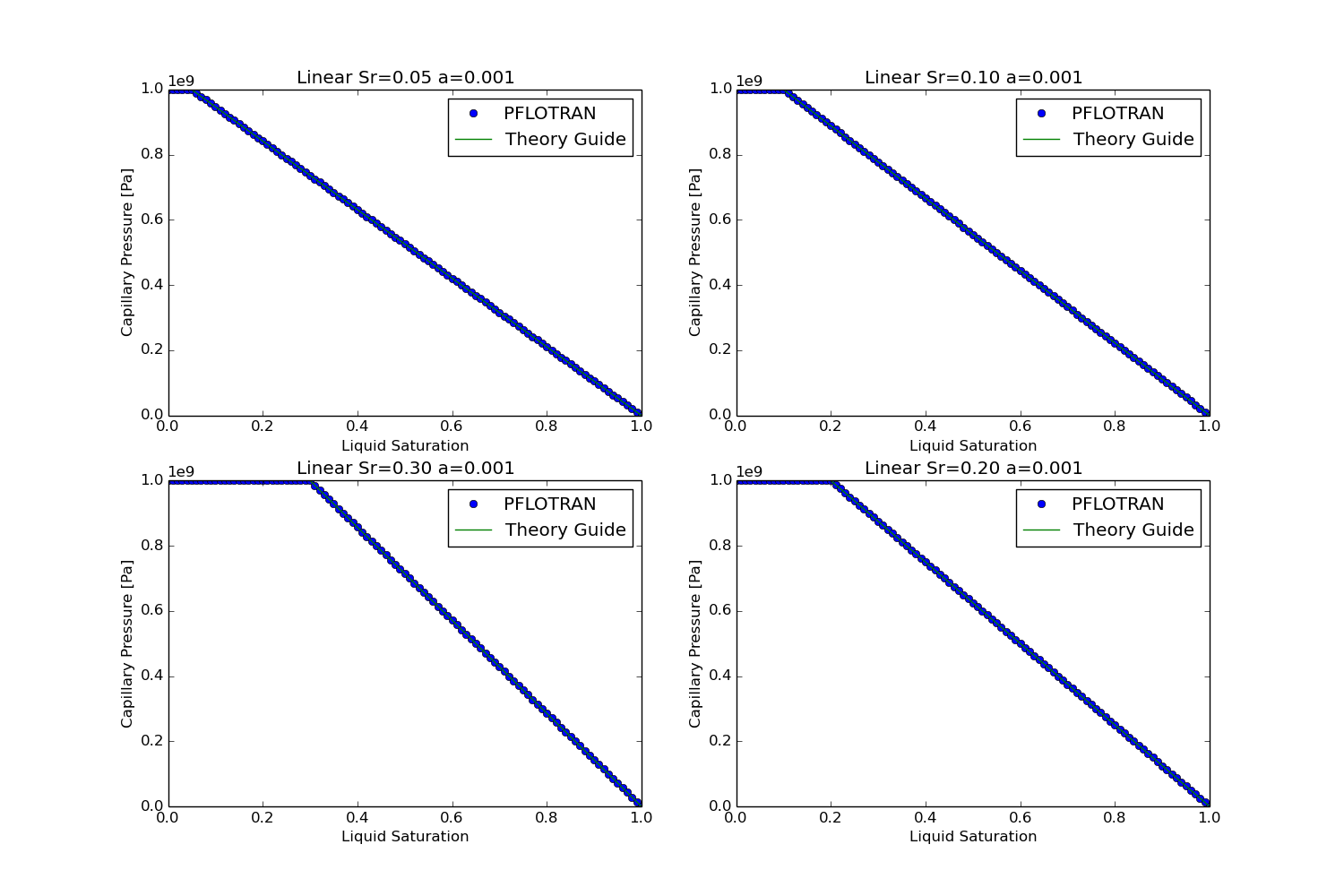
The following plots show a visual comparison between the PFLOTRAN implementation of the capillary pressure and saturation functions, and the equation for these functions as given in Chen et al. (1999), or the Theory Guide in the case of the linear relationships. The results of the SMOOTH option is also tested for the Brooks-Corey relationships. For the linear saturation function relationship, the value of alpha given does not modify the solution significantly, therefore, the value of alpha is held constant, while the liquid residual saturation is varied between 0.05 and 0.30.
Chen, J., J. W. Hopmans, and M. E. Grismer (1999) Parameter estimation of two-fluid capillary pressure-saturation and permeability functions, Advances in Water Resources, Vol. 22, No. 5, pp. 479-493.
Brooks-Corey¶
This option is specified with SATURATION_FUNCTION BROOKS_COREY in the
CHARACTERISTIC_CURVES card.
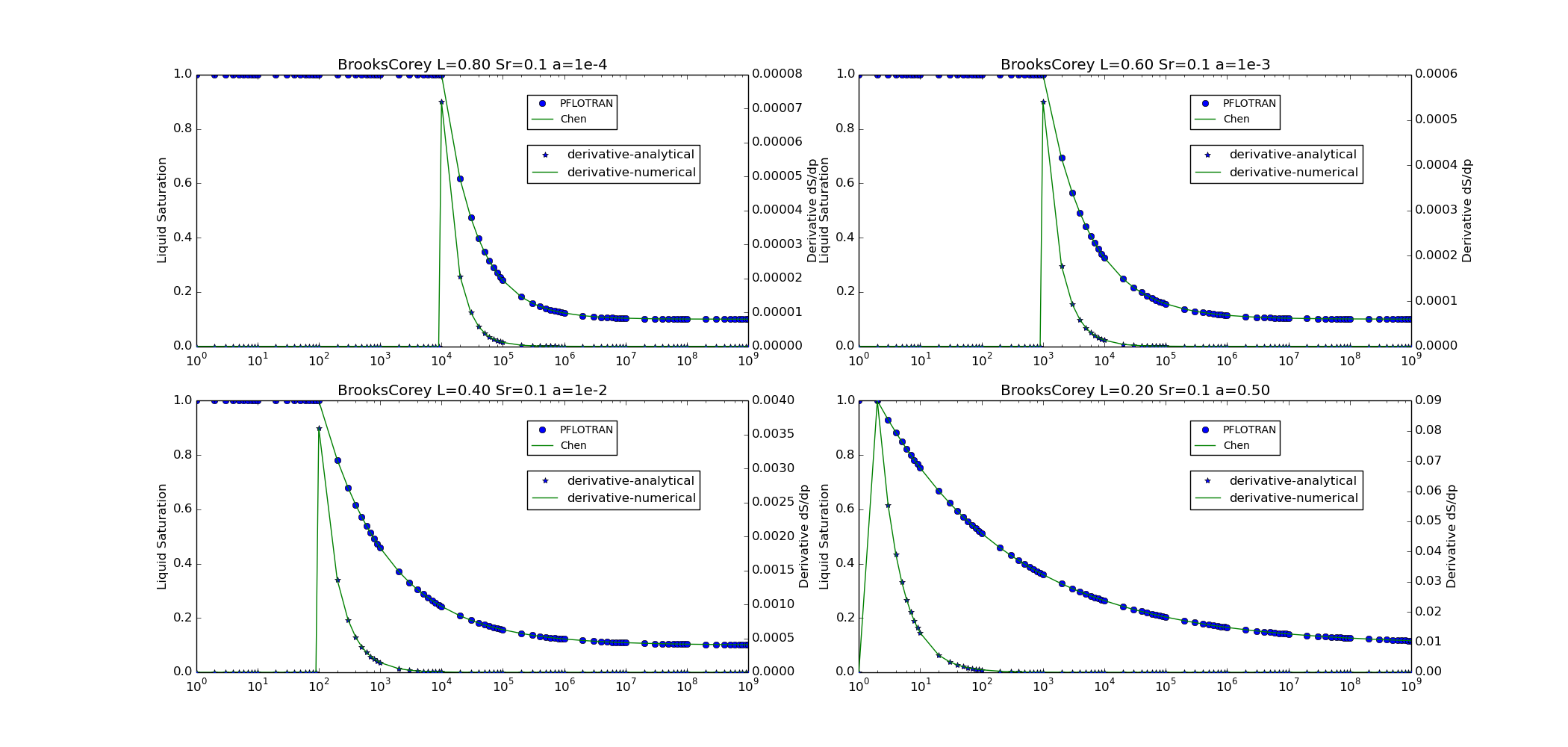

Note, similar relationships are used for the SATURATION_FUNCTION options
BRAGFLO_KRP2, BRAGFLO_KRP3, BRAGFLO_KRP4, and BRAGFLO_KRP12 options,
with minor tweaks.
KRP2¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP2,
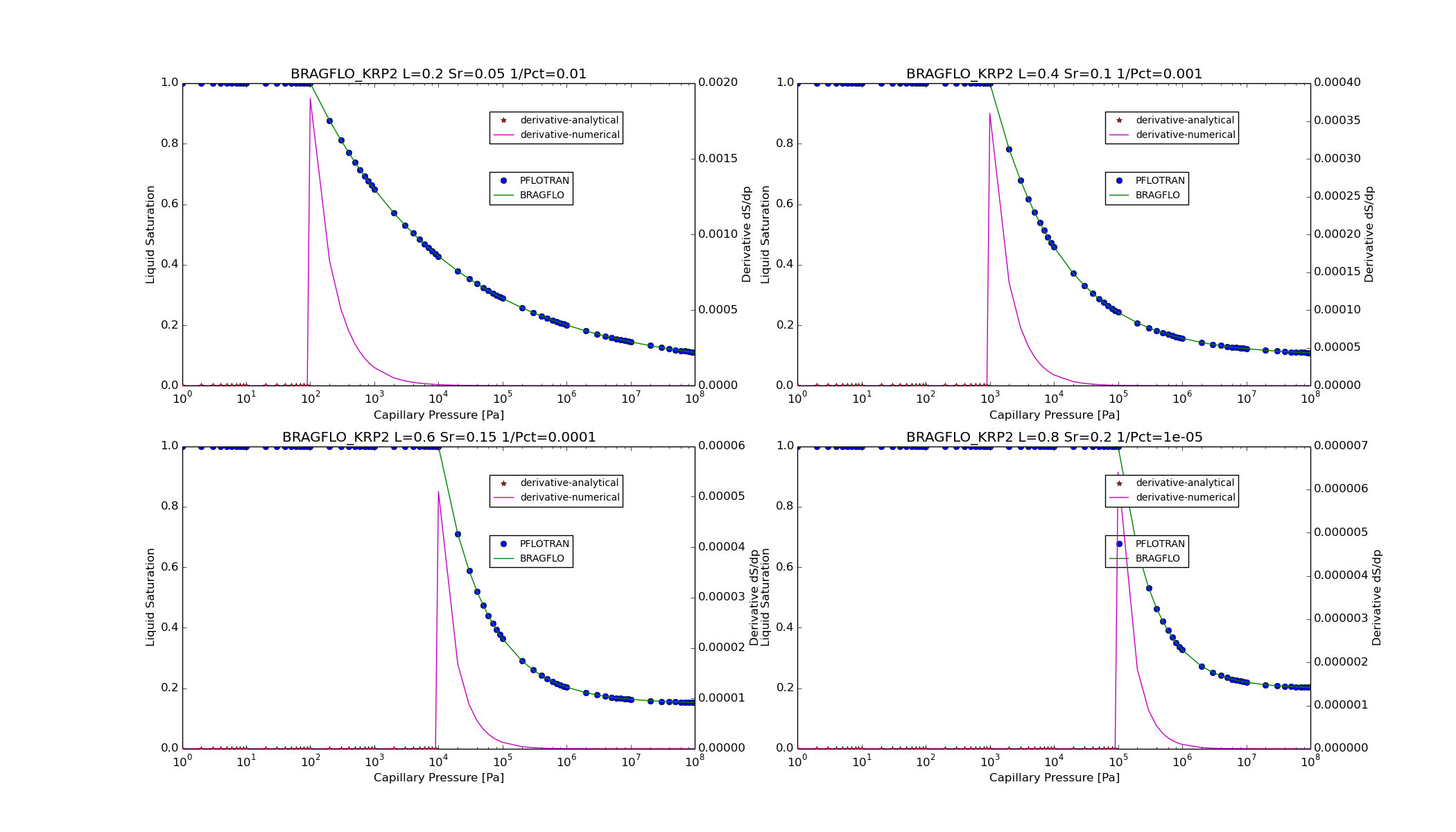
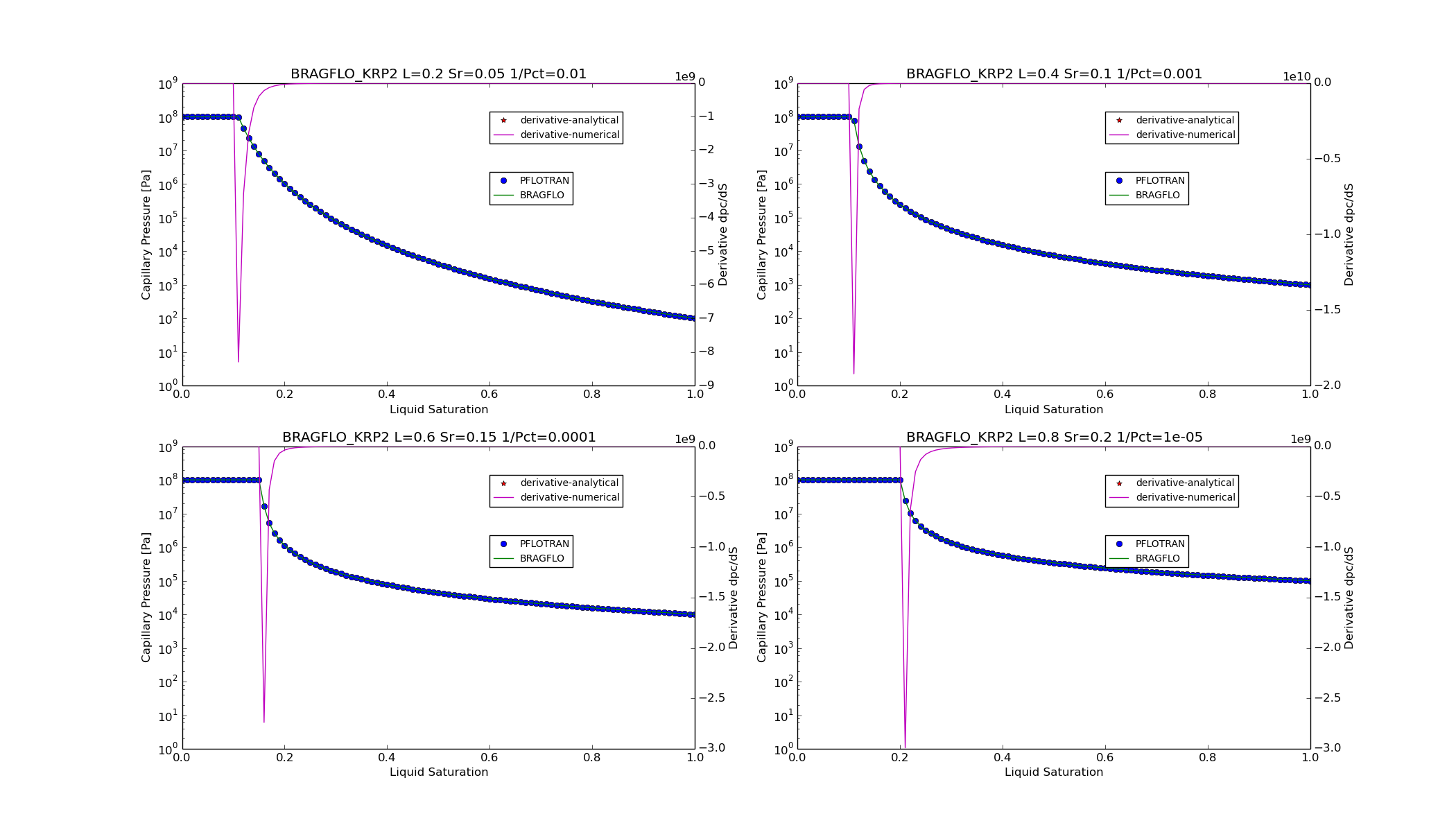
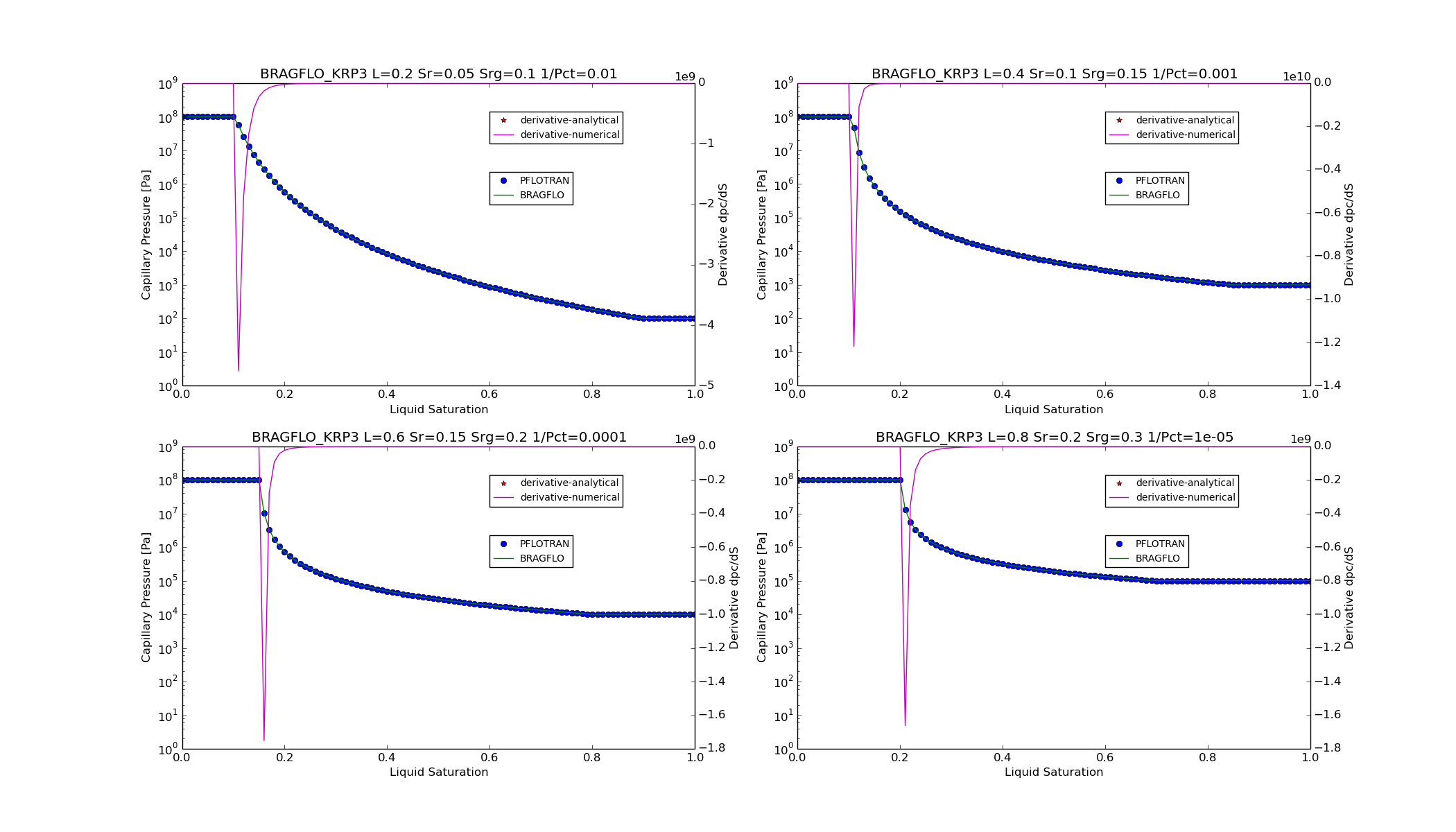
KRP3¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP3,
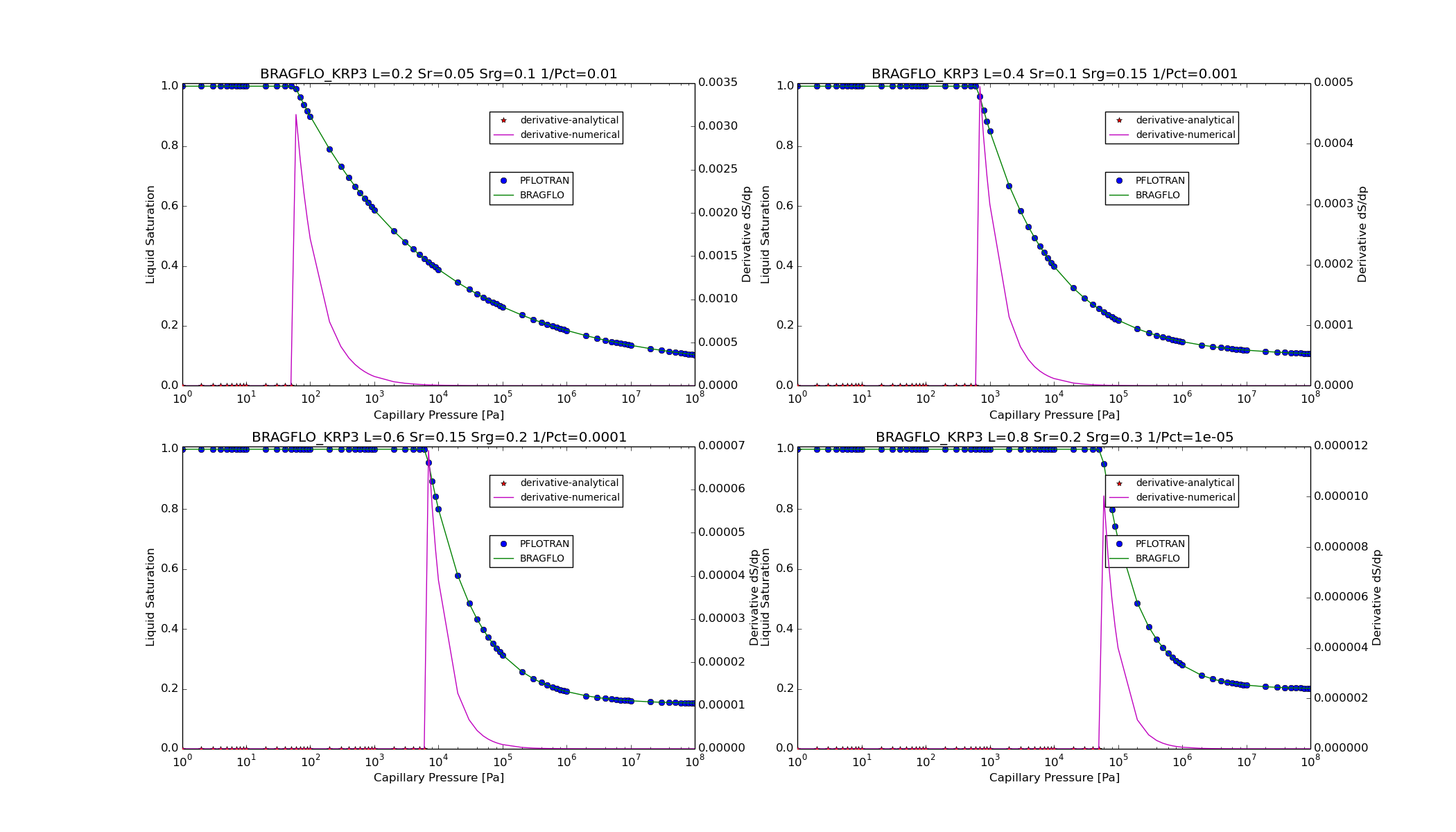
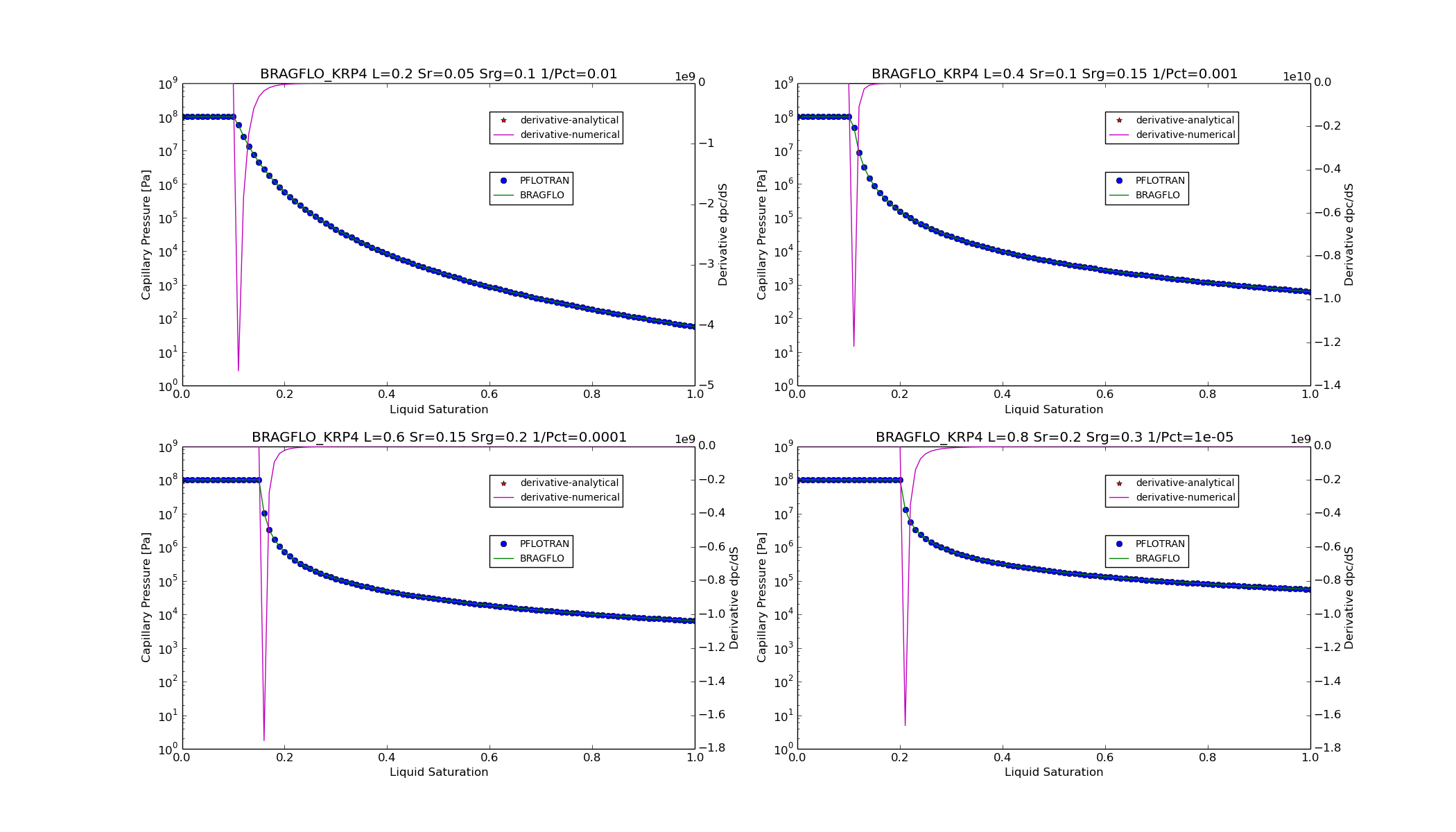
KRP4¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP4,

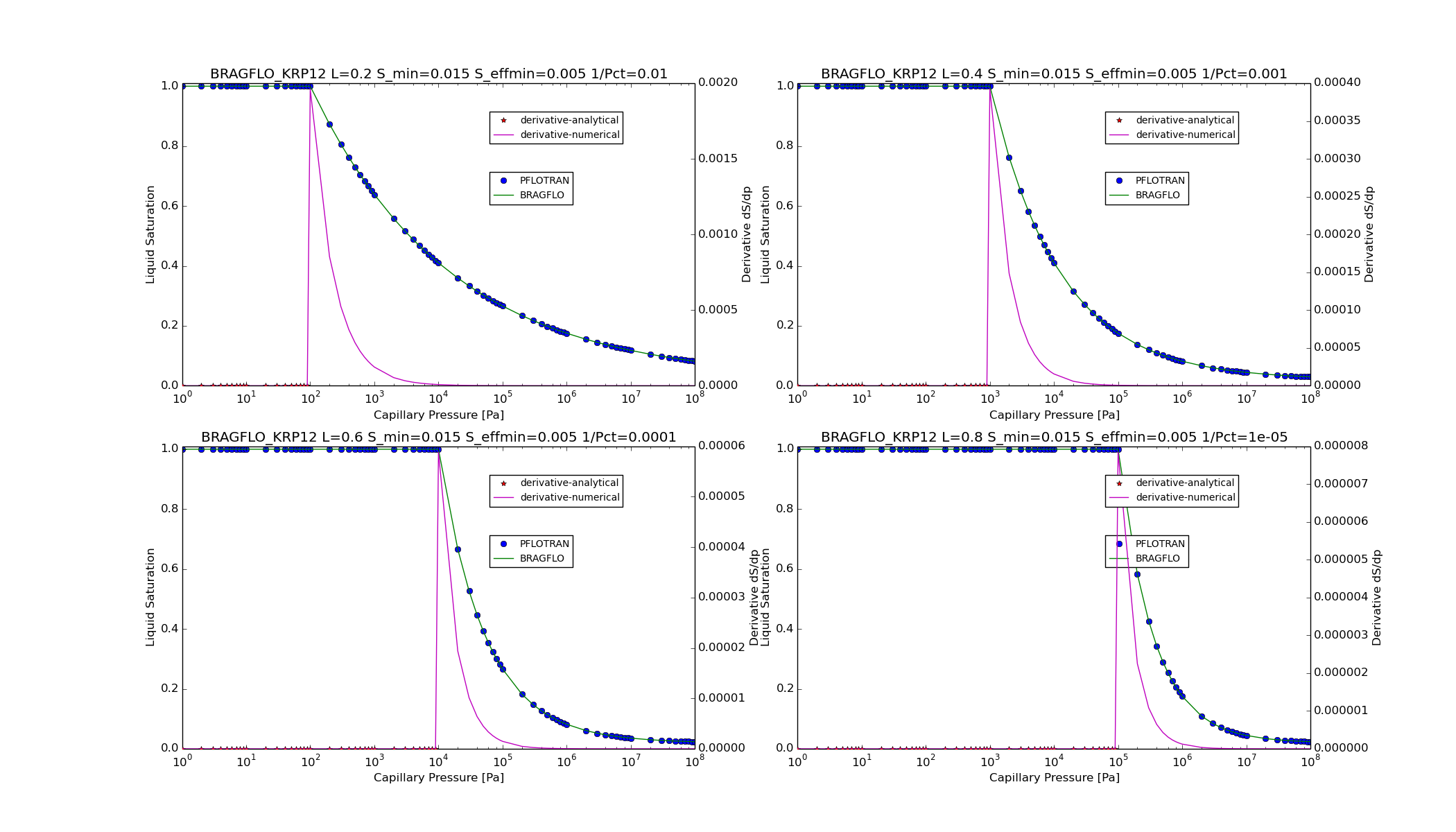
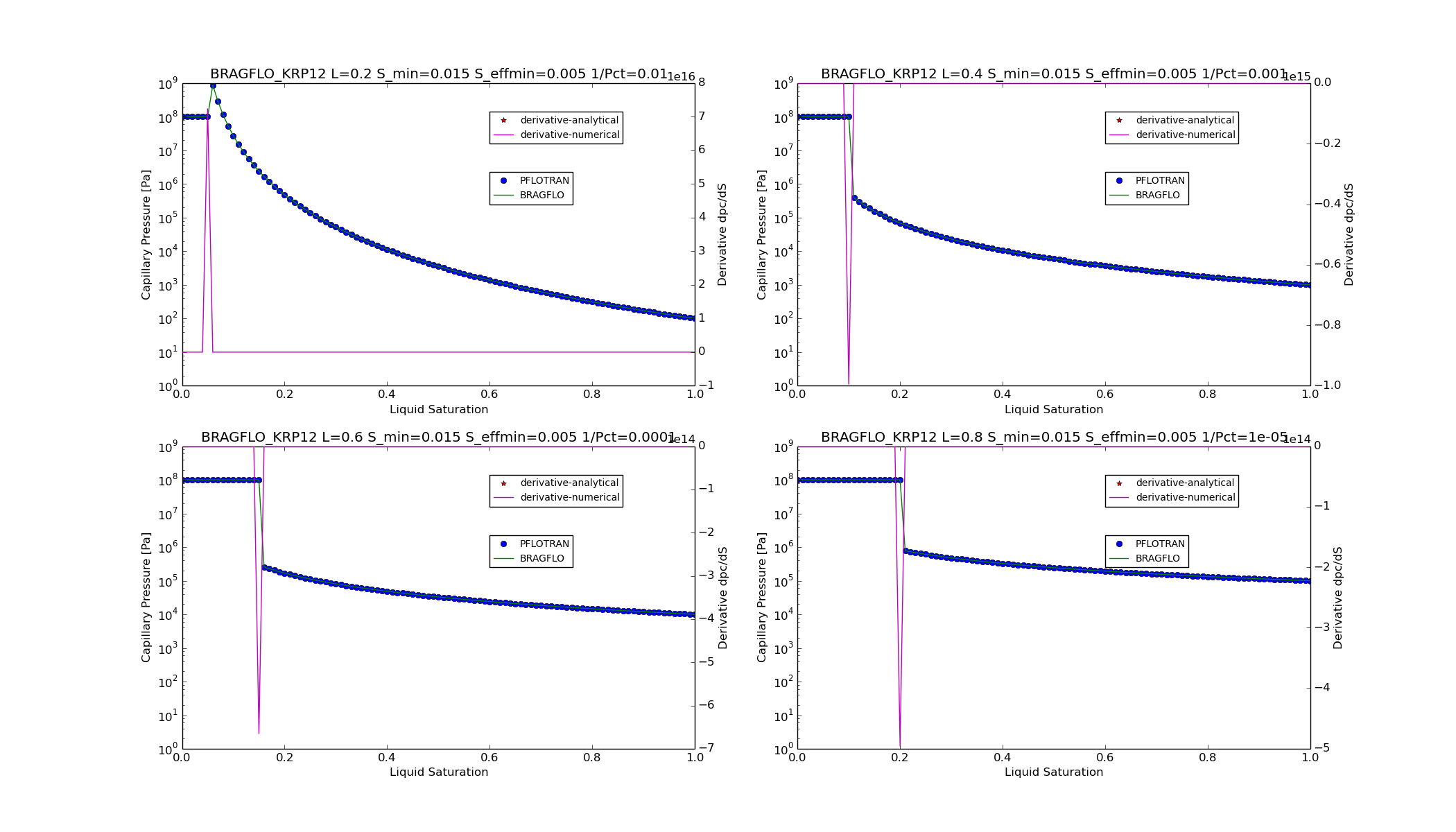
KRP12¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP12,
The value of \(S_{e21}\) is not allowed to go above 1.0 or below \(S_{EFFMIN}\).
van Genuchten¶
This option is specified with SATURATION_FUNCTION VAN_GENUCHTEN in the
CHARACTERISTIC_CURVES card.
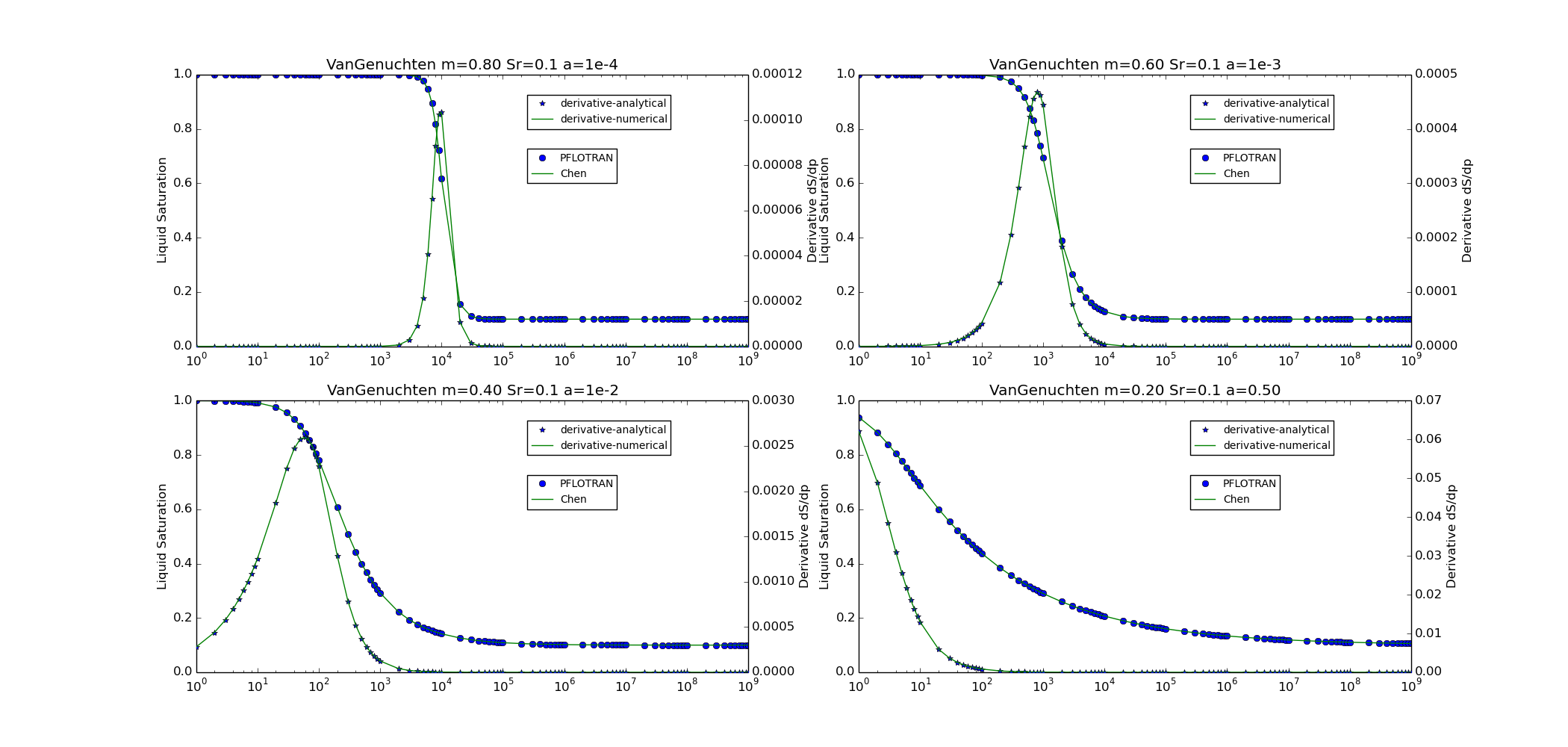
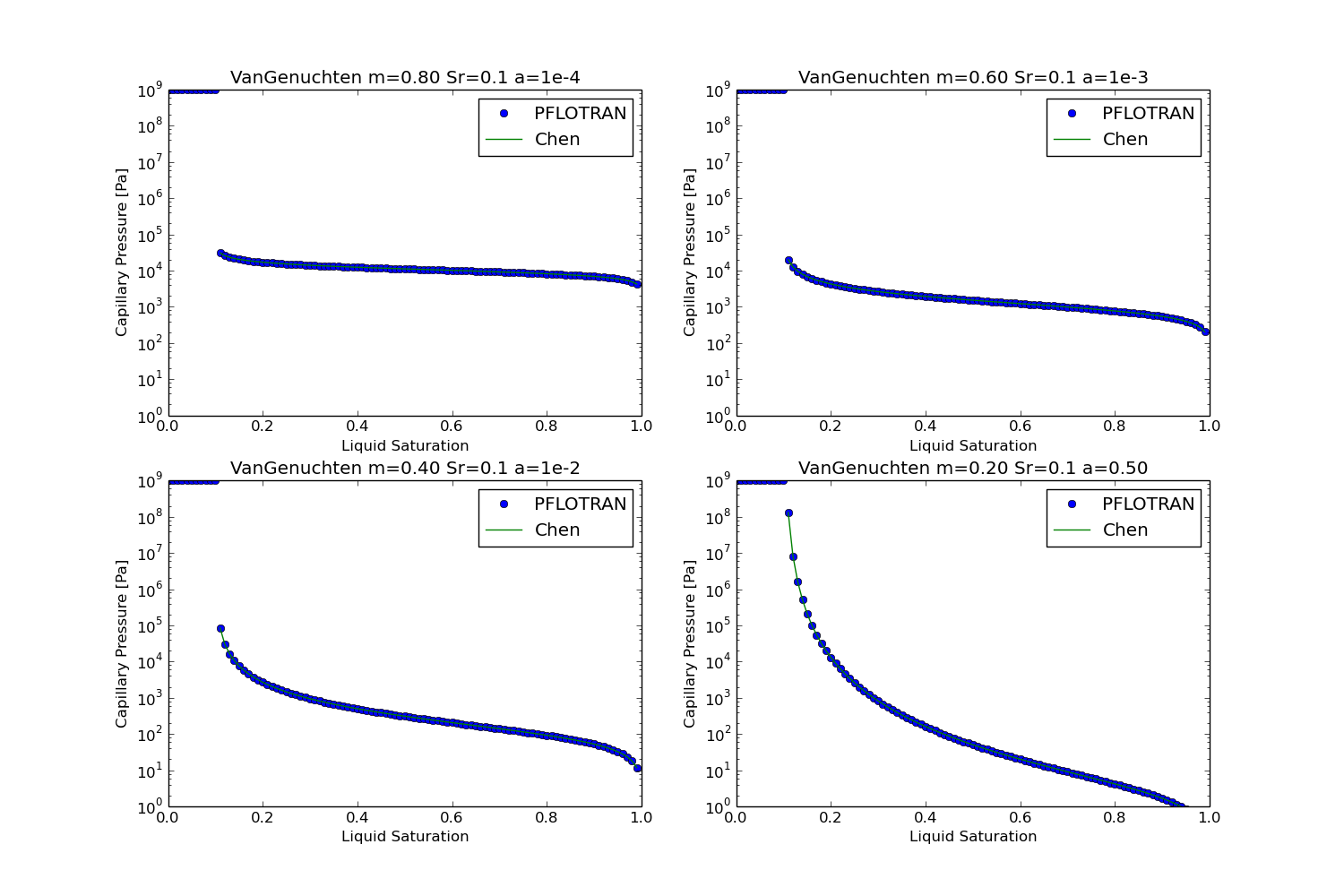
Note, similar relationships are used for the SATURATION_FUNCTION options
BRAGFLO_KRP1 and BRAGFLO_KRP8 options, with minor tweaks.
KRP1¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP1,
where the parameter \(p_0\) is derived by setting \(S_{eg}\) in the KRP4 and KRP1 capillary pressure saturation relationships to 0.5, equating the KRP4 to the KRP1 relationship, and then solving for \(p_0\) in the KRP1 side of the relationship, e.g.,
The value of \(S_{e2}\) is not allowed to go over 1.0.

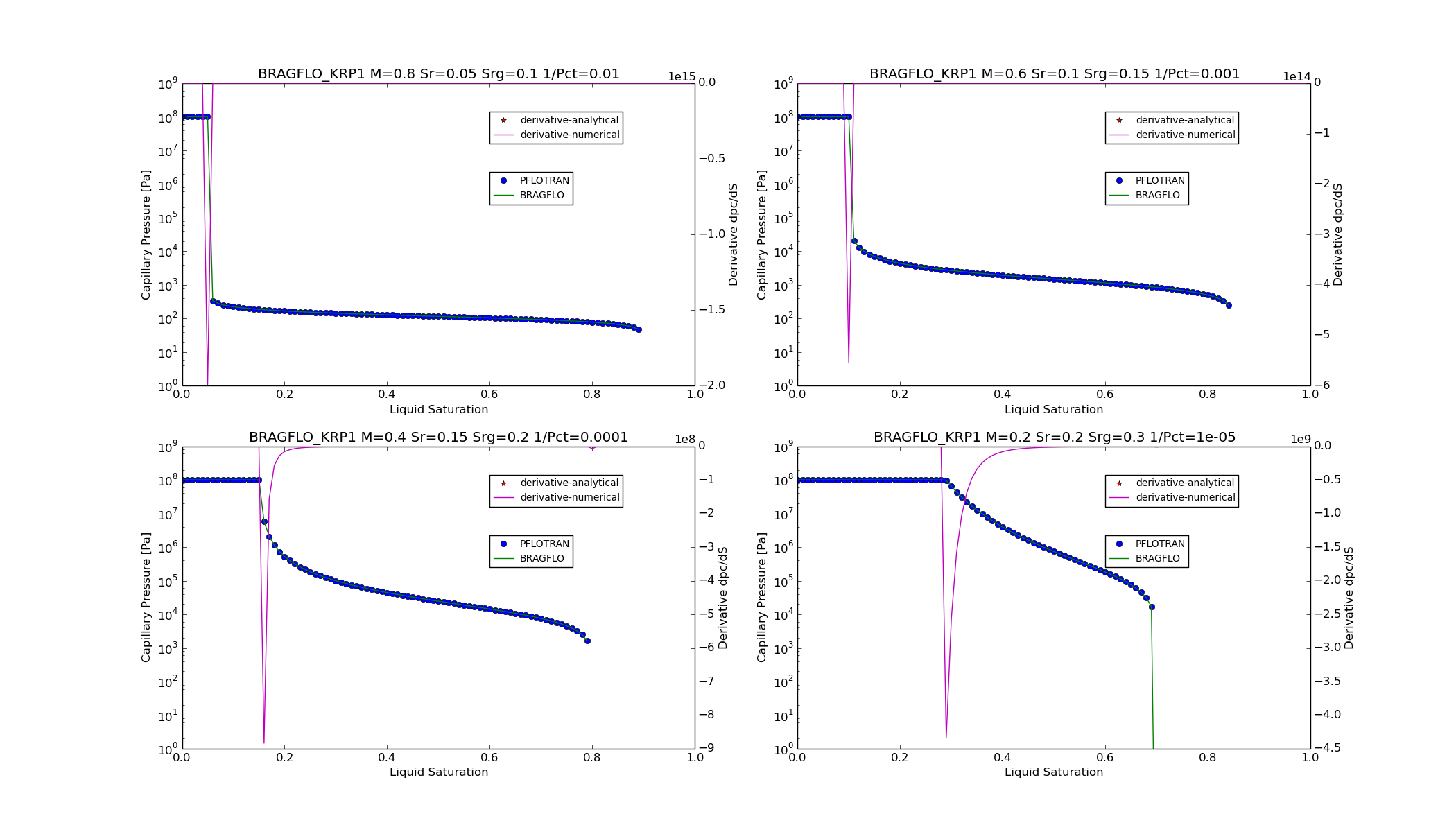
KRP8¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP8,


Linear¶
This option is specified with SATURATION_FUNCTION LINEAR in the
CHARACTERISTIC_CURVES card.
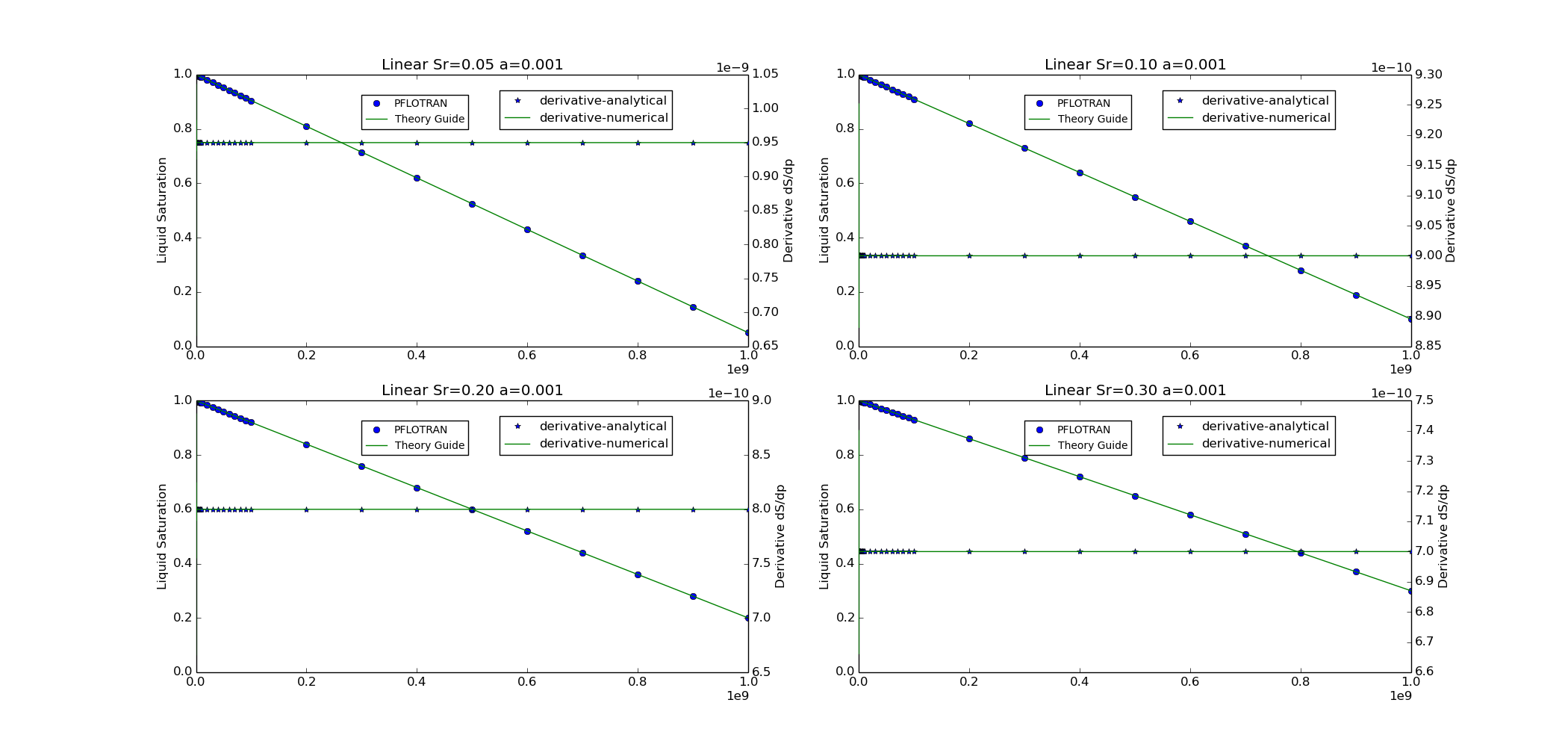
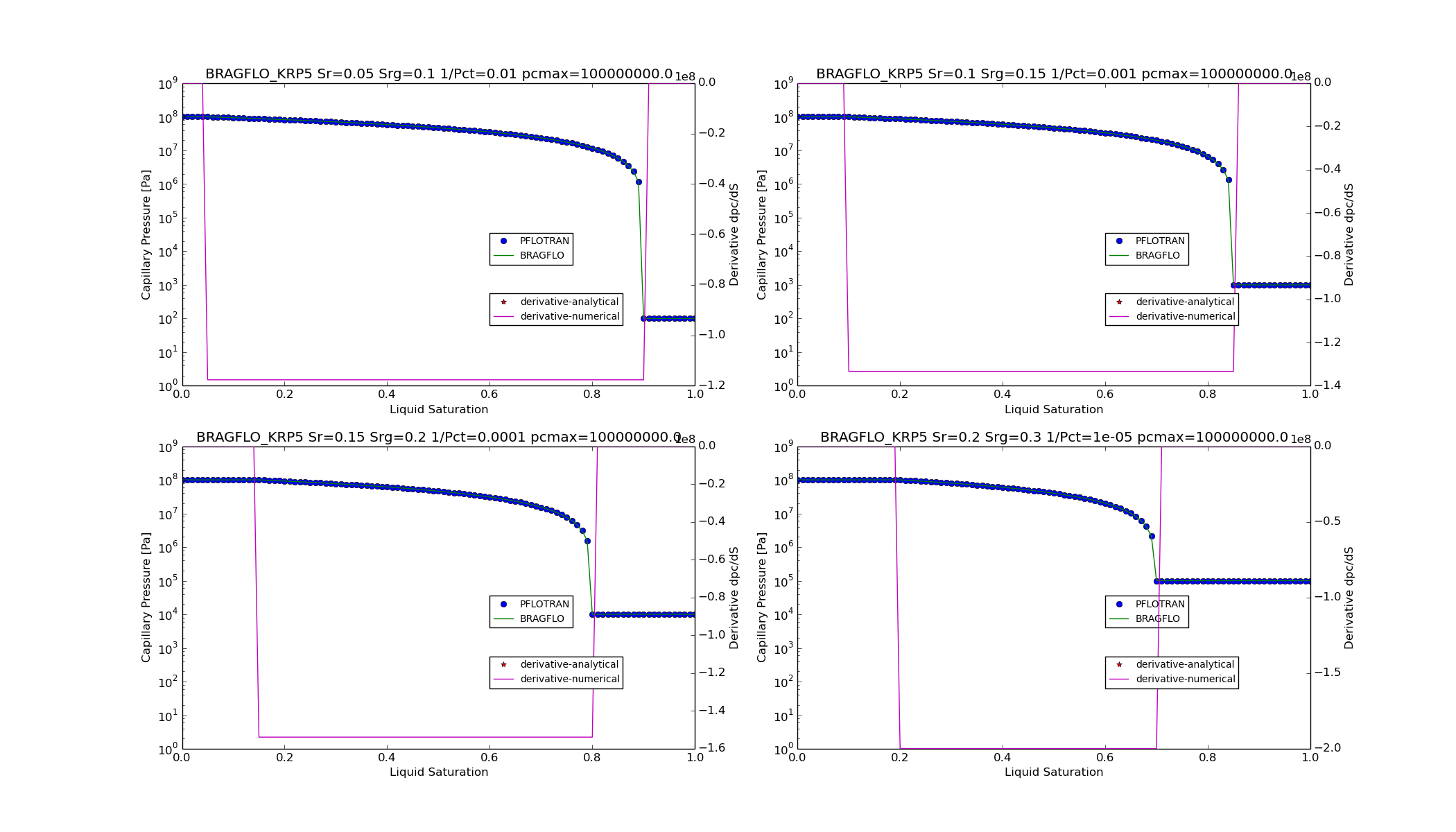
KRP5¶
For option CHARACTERISTIC_CURVES
SATURATION_FUNCTION BRAGFLO_KRP5,

Vauclin et al. (KRP9)¶
This option is specified with SATURATION_FUNCTION BRAGFLO_KRP9 in the
CHARACTERISTIC_CURVES card.
where parameters \(a=3783.0145\) and \(b=2.9\)


Open Cavity Modification (KRP11)¶
This option is specified with SATURATION_FUNCTION BRAGFLO_KRP11 in the
CHARACTERISTIC_CURVES card. It simply sets the capillary pressure
to zero and the liquid saturation to unity.
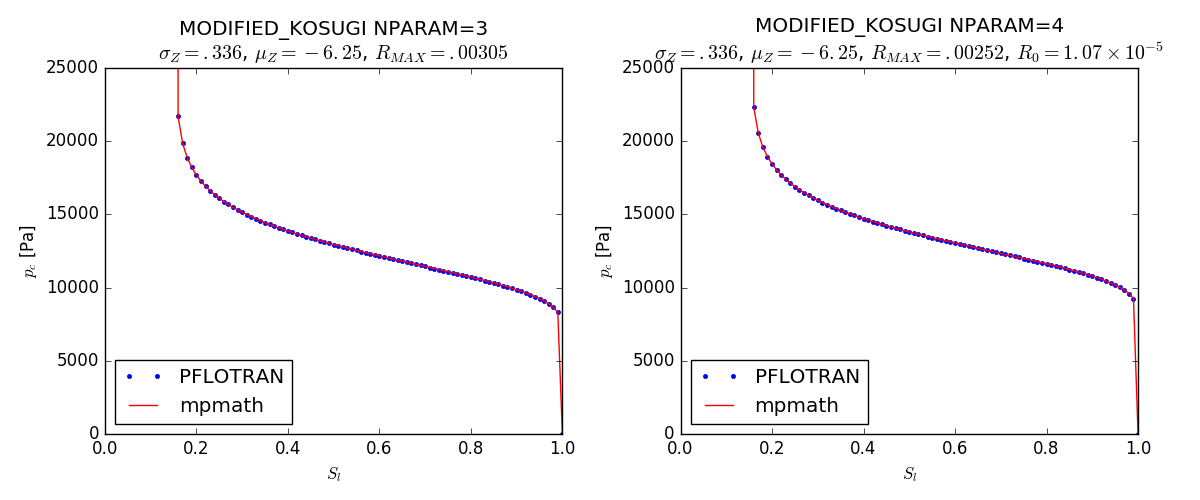
Modified Kosugi¶
This option is specified with SATURATION_FUNCTION MODIFIED_KOSUGI in
the CHARACTERISTIC_CURVES card.
where \(\kappa=0.149 \; \mathrm{[cm^2]}\) is a constant from the Young-Laplace equation (\(2\gamma\)), \(\mathrm{log}\) is the base-\(e\) logarithm, and \(\mathrm{erfc}\) is the complimentary error function. Given the parameters \(\sigma_Z=0.336\), \(\mu_Z=-6.25\), \(S_{rl}=0.153\), the following figures illustrate the function and its derivatives over a range of saturation and capillary pressures.

Testing Results For Relative Permeability Functions¶
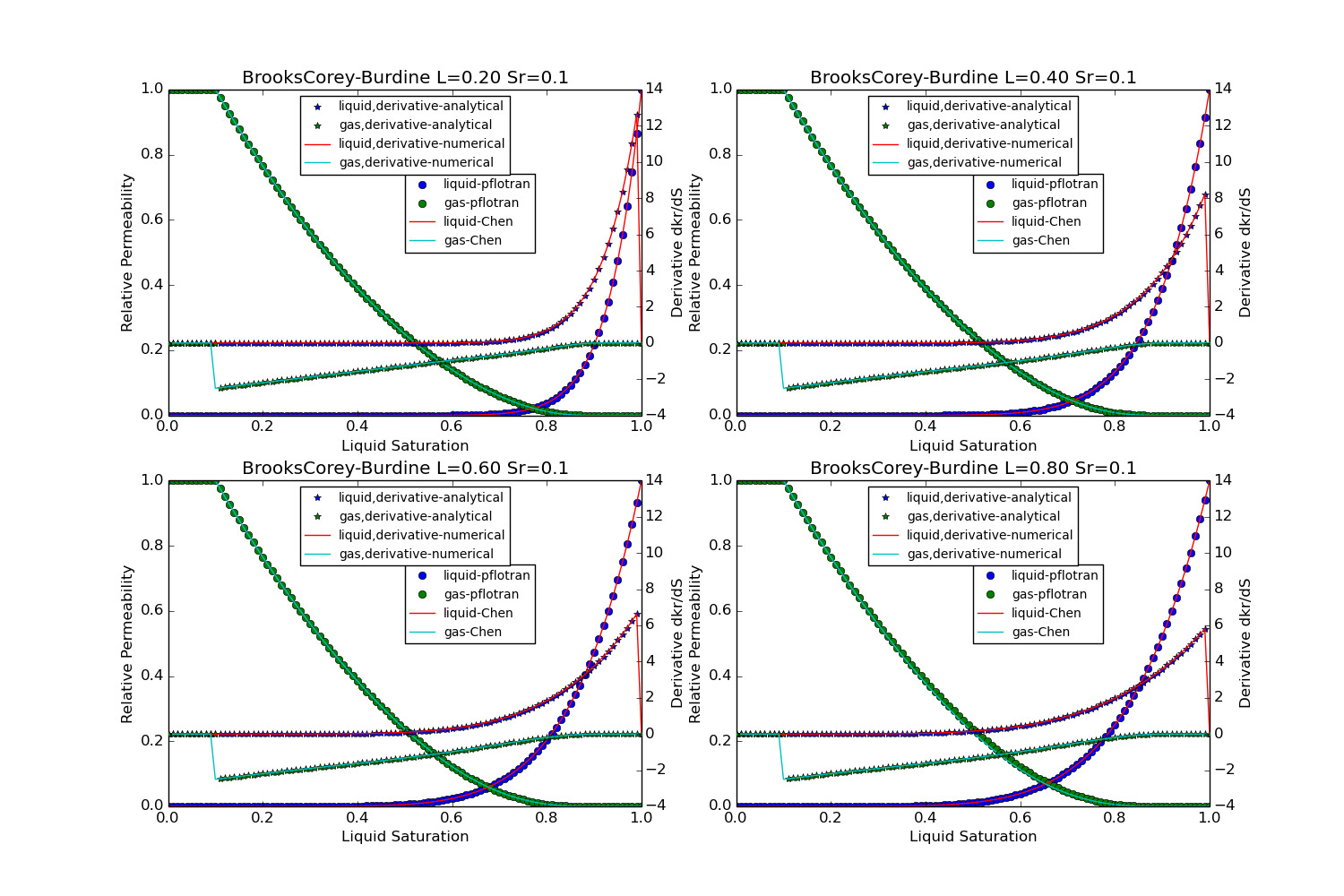
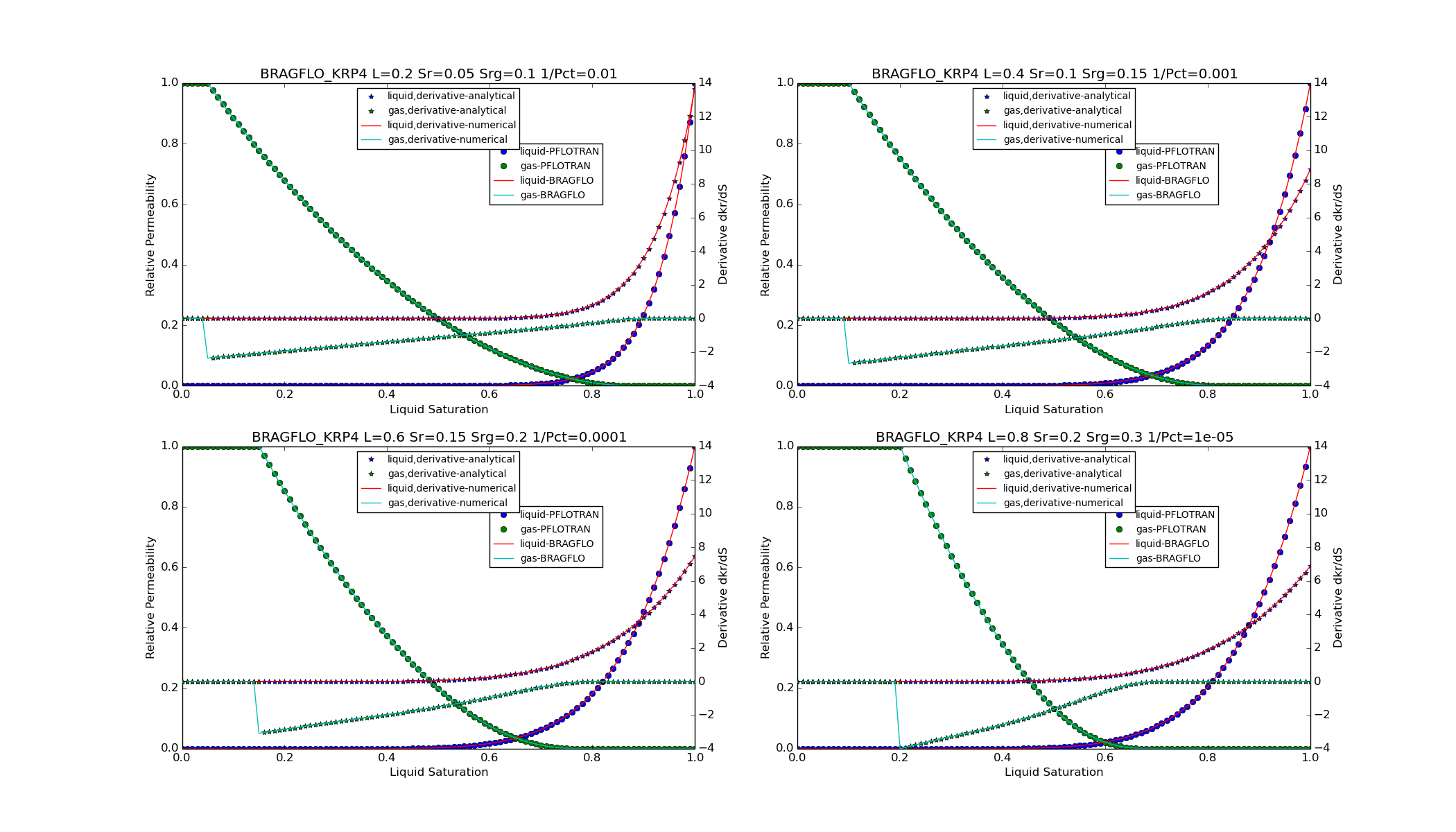
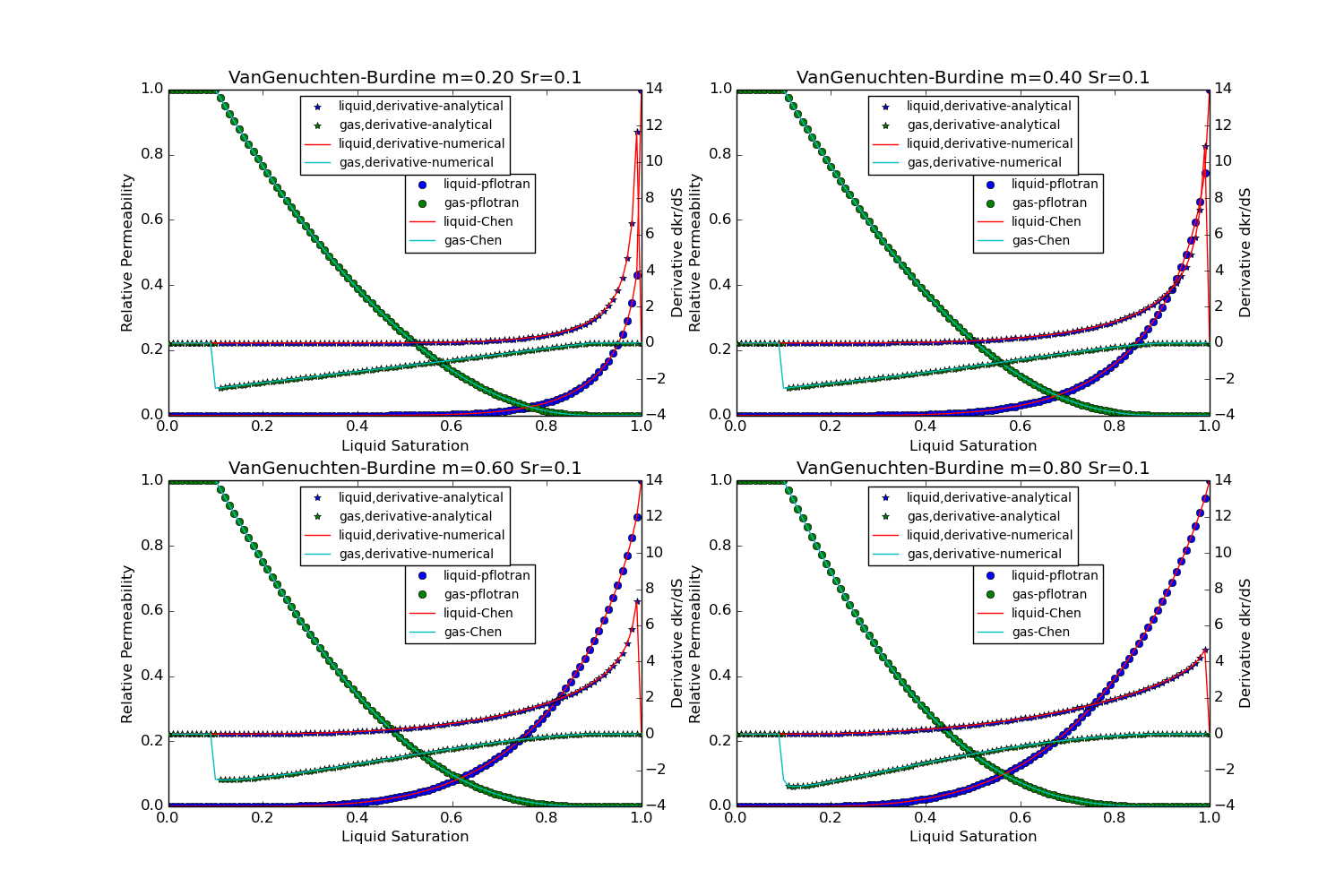
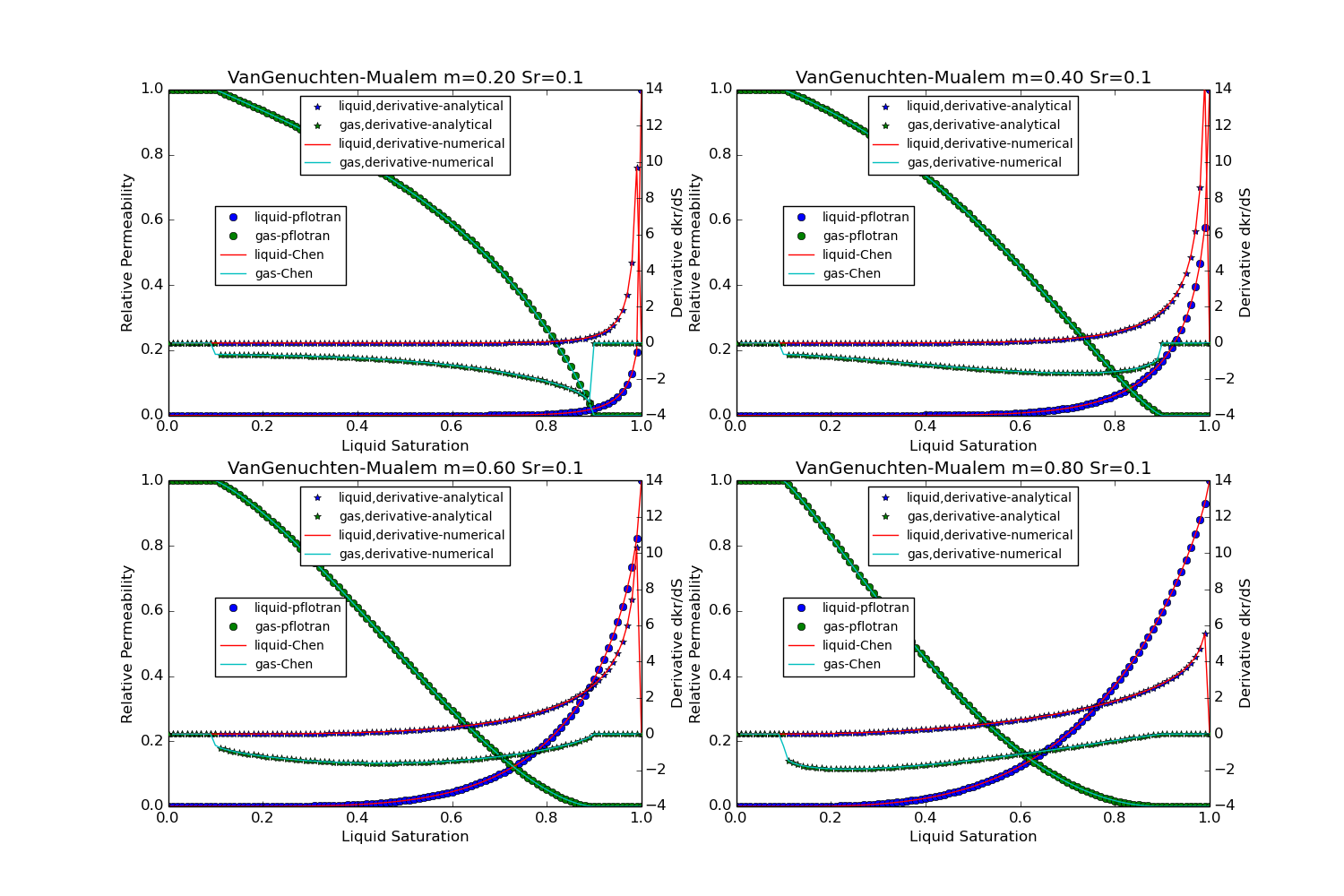
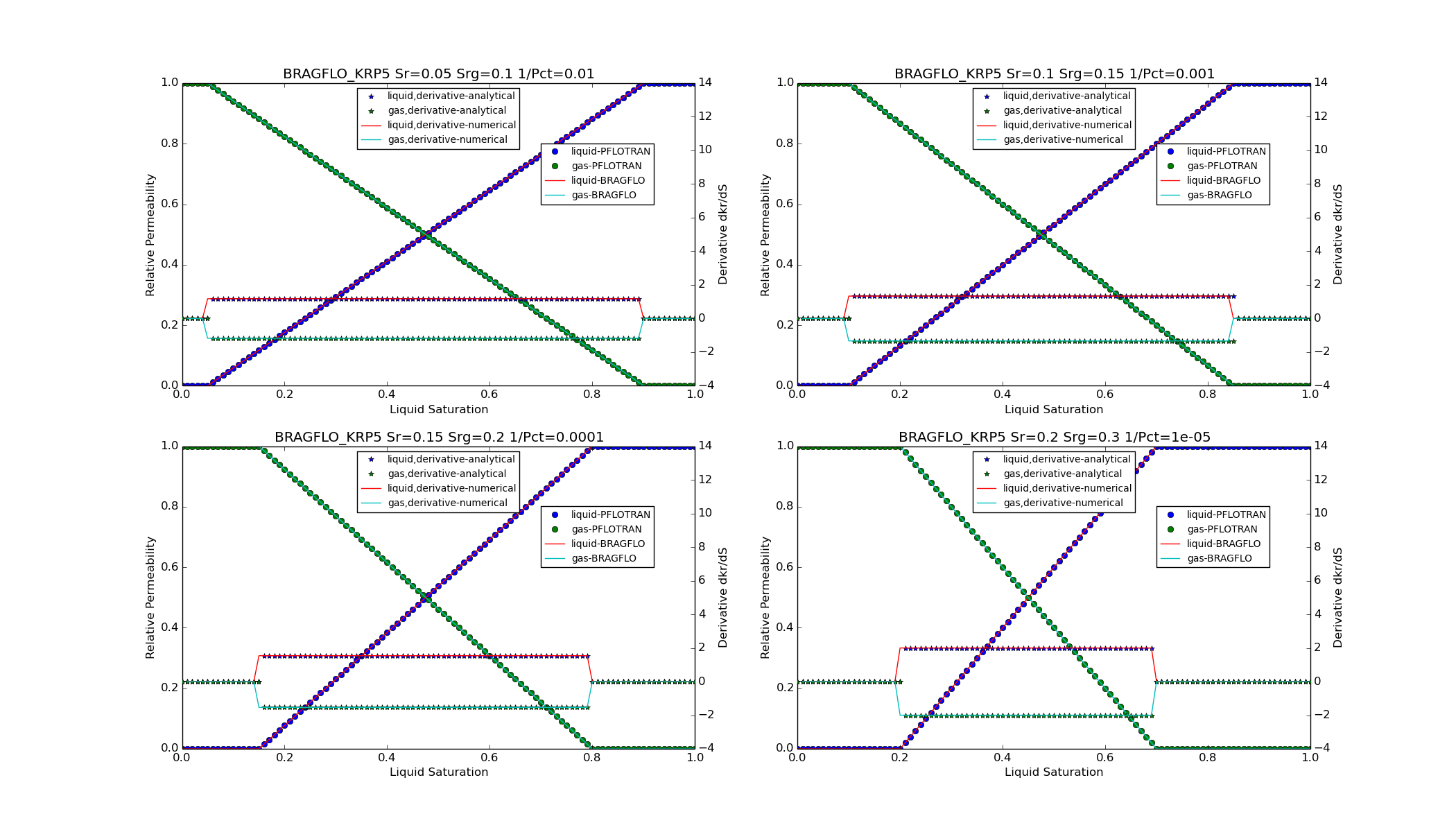
The following plots show a visual comparison between the PFLOTRAN implementation of the relative permeability functions, and the equation for the relative permeability as given in Chen et al. (1999), the Theory Guide, or BRAGFLO. The linear Mualem curves remain untested against the thoery guide, but they are plotted.
Chen, J., J. W. Hopmans, and M. E. Grismer (1999) Parameter estimation of two-fluid capillary pressure-saturation and permeability functions, Advances in Water Resources, Vol. 22, No. 5, pp. 479-493.
Brooks-Corey-Burdine¶
This option is specified with PERMEABILITY_FUNCTION BURDINE_BC_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.
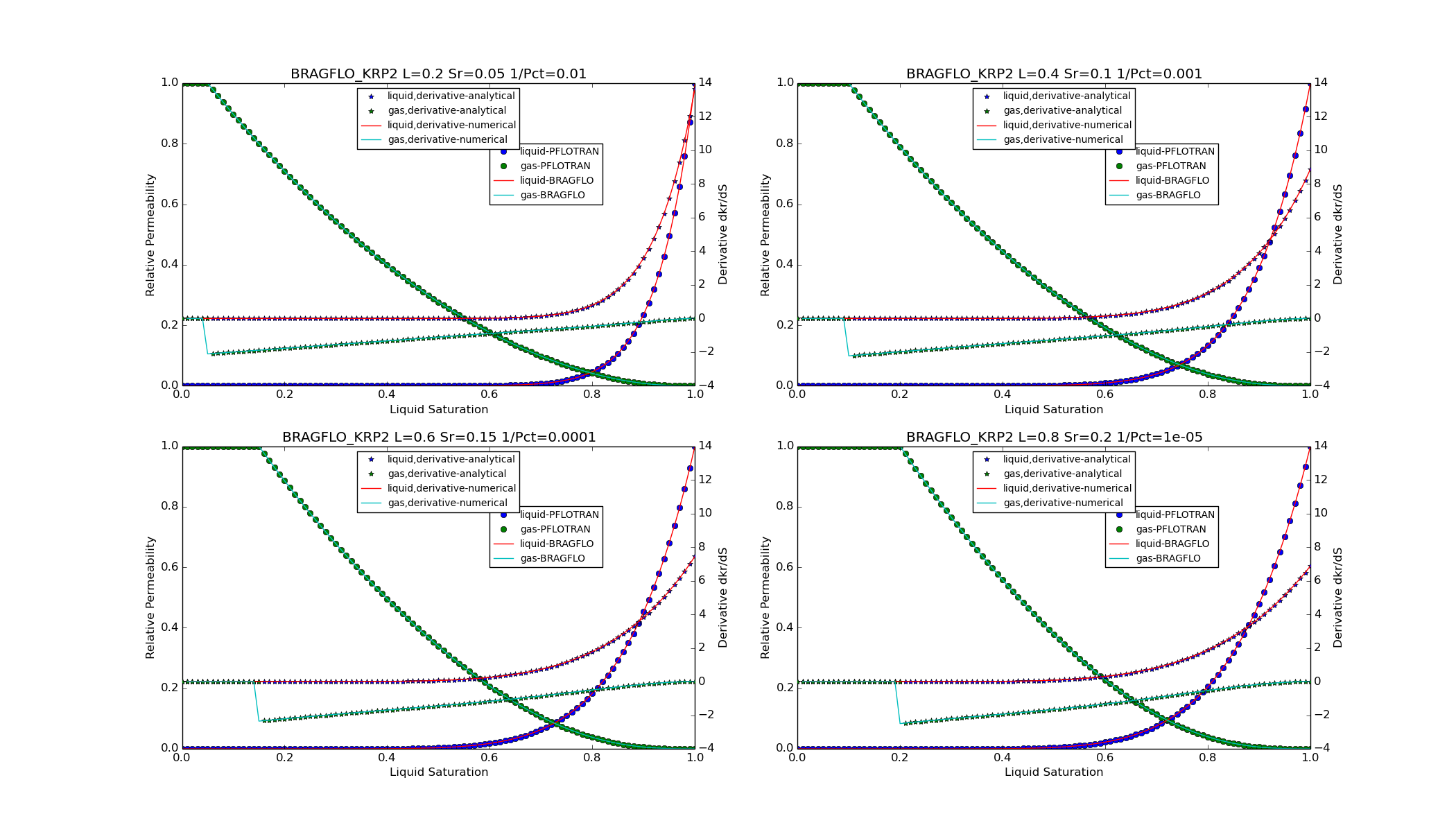
KRP2¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP2_[LIQ/GAS],
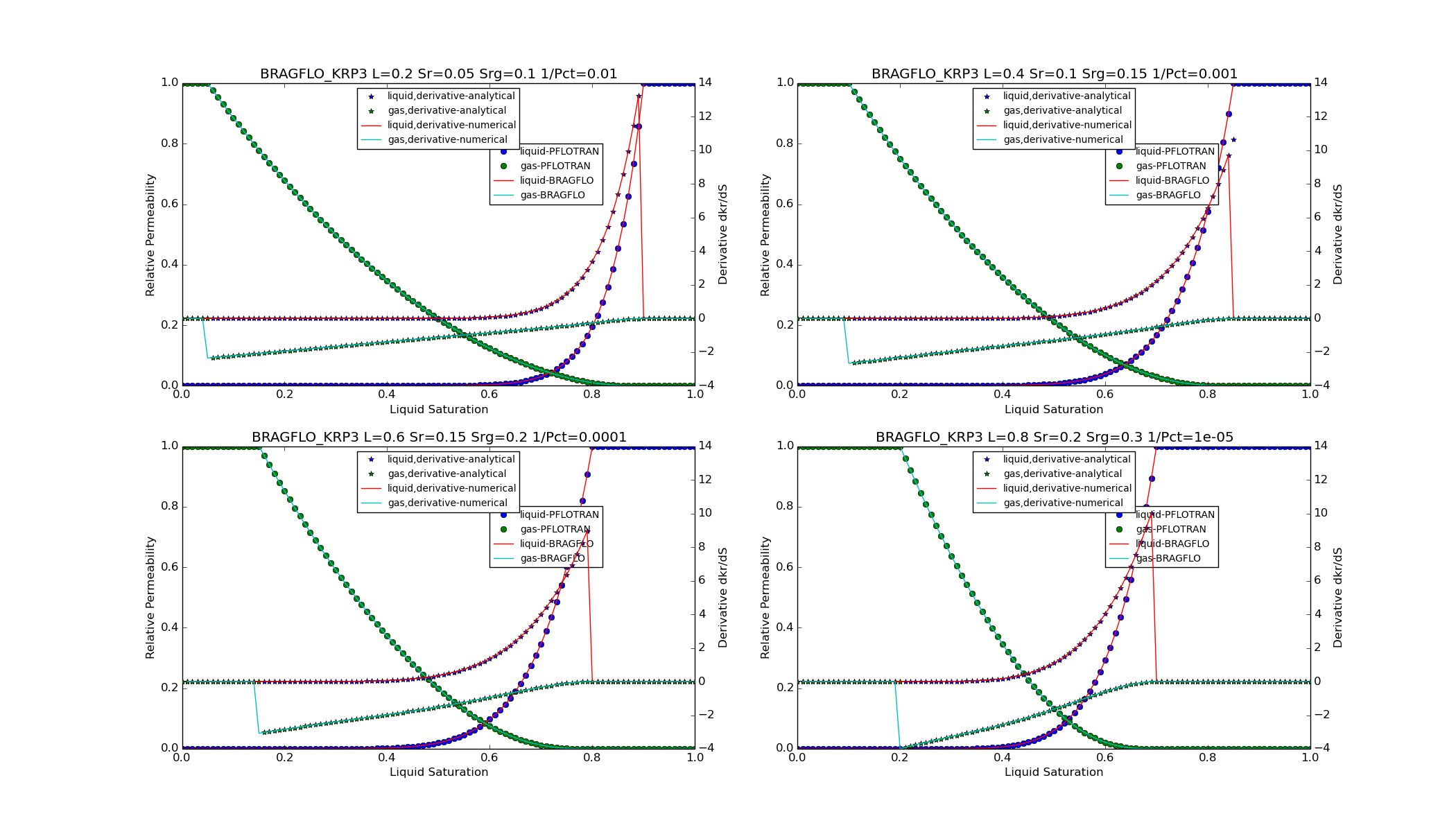
KRP3¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP3_[LIQ/GAS],
KRP4¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP4_[LIQ/GAS],
KRP12¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP12_[LIQ/GAS],

Brooks-Corey-Mualem¶
This option is specified with PERMEABILITY_FUNCTION MUALEM_BC_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.

van Genuchten-Burdine¶
This option is specified with PERMEABILITY_FUNCTION BURDINE_VG_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.
van Genuchten-Mualem¶
This option is specified with PERMEABILITY_FUNCTION MUALEM_VG_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.
KRP1¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP1_[LIQ/GAS],

KRP8¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP8_[LIQ/GAS],

Linear-Burdine¶
This option is specified with PERMEABILITY_FUNCTION BURDINE_LINEAR_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.

KRP5¶
For option CHARACTERISTIC_CURVES
PERMEABILITY_FUNCTION BRAGFLO_KRP5_[LIQ/GAS],
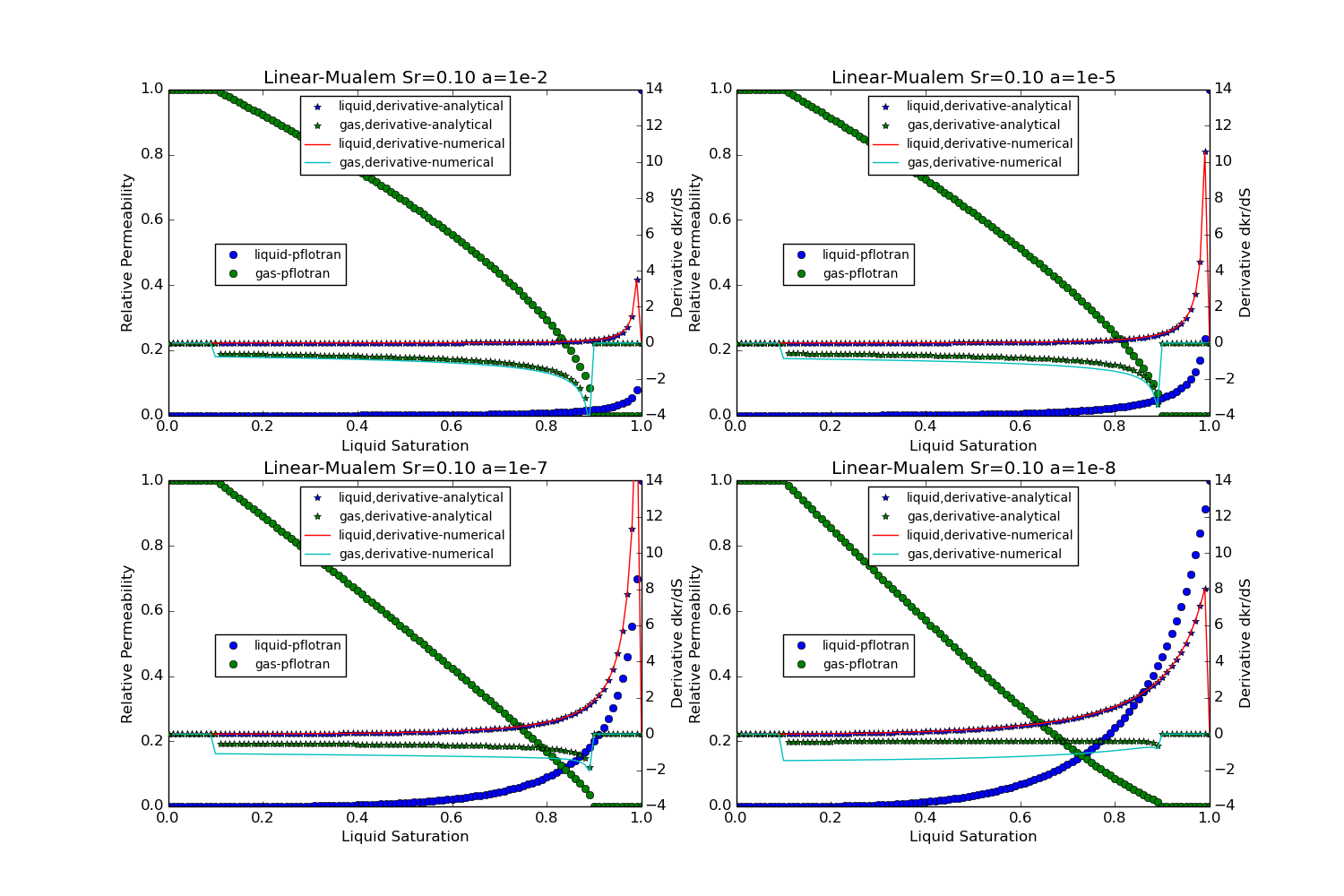
Linear-Mualem¶
This option is specified with PERMEABILITY_FUNCTION MUALEM_LINEAR_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.
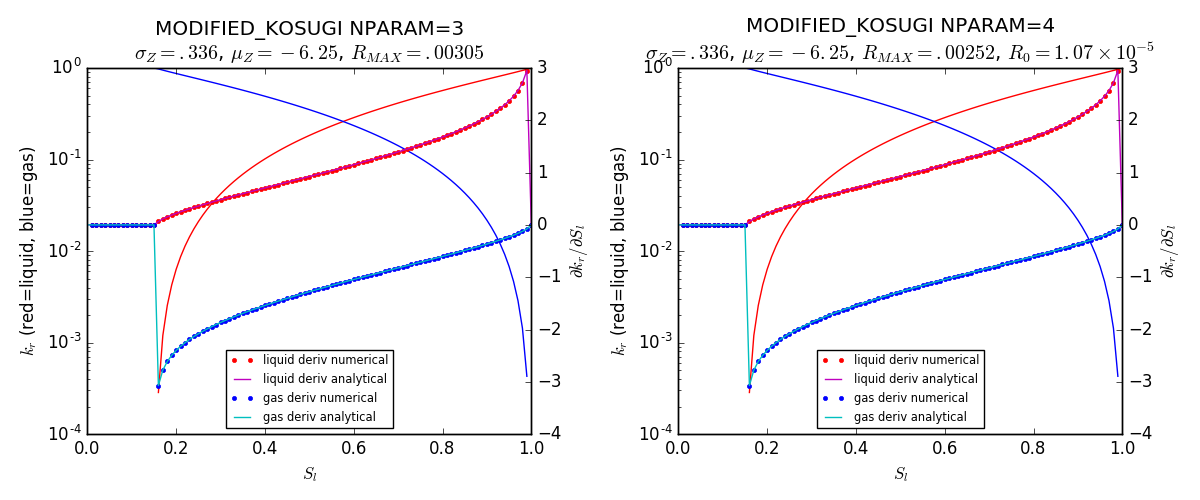
Modified Kosugi¶
This option is specified with PERMEABILITY_FUNCTION MODIFIED_KOSUGI_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card
where \(\mathrm{erfc^{-1}}\) is the inverse complimentary error function. Given the parameters \(\sigma_Z=0.336\), \(\mu_Z=-6.25\), \(S_{rl}=0.153\), and \(S_{rg}=0.001\), the following figure illustrates the function and its derivatives over a range of liquid saturation.
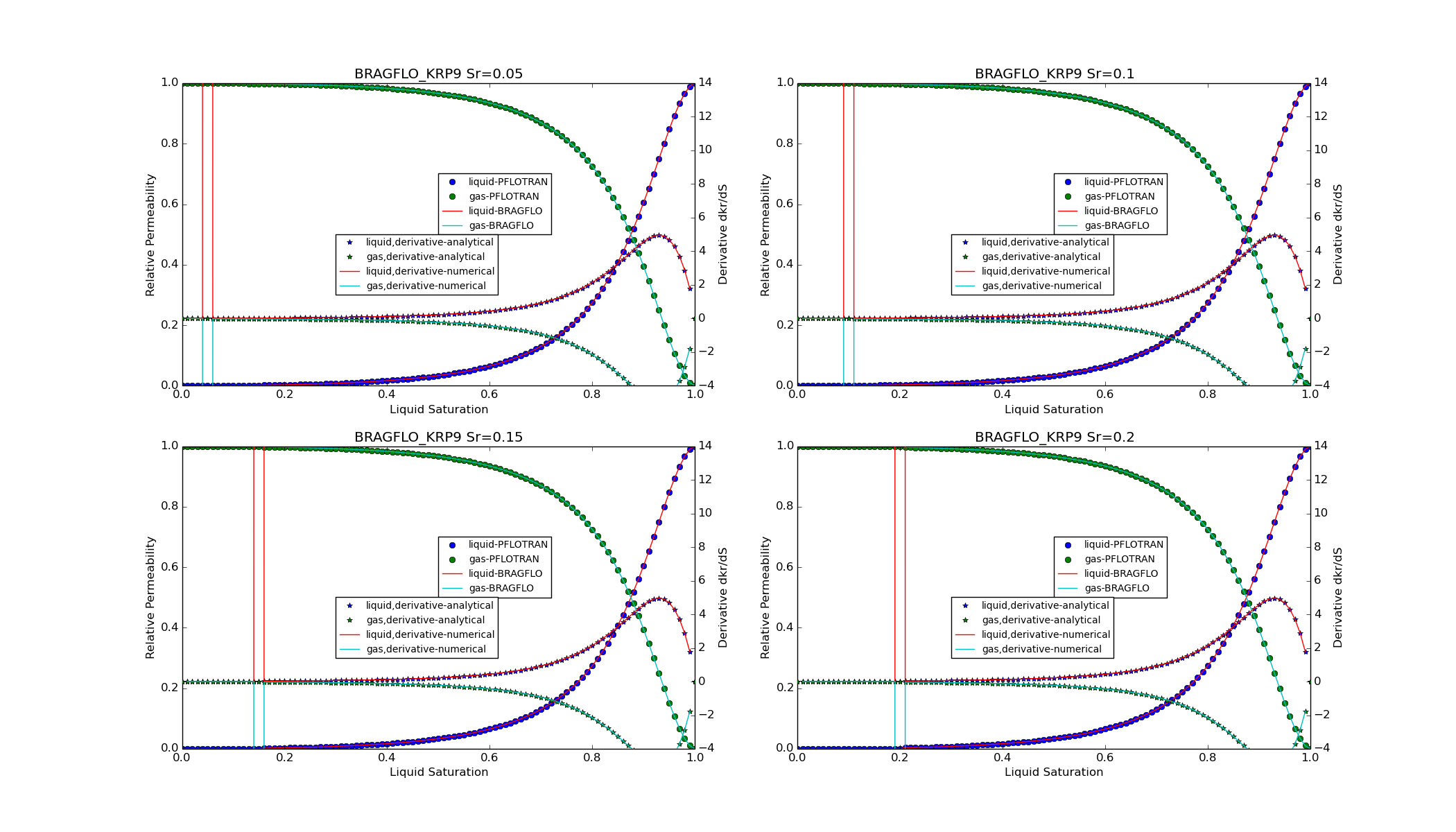
Vauclin et al. (KRP9)¶
This option is specified with PERMEABILITY_FUNCTION BRAGFLO_KRP9_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.
where the parameters \(a=28.768353\) and \(b=1.7241379\).
Open Cavity Modification (KRP11)¶
This option is specified with PERMEABILITY_FUNCTION BRAGFLO_KRP11_[LIQ/GAS]
in the CHARACTERISTIC_CURVES card.

